1387. Подземные кабеля

Город хочет избавиться от своих неприглядных электроопор, переместив силовые кабели под землю. Имеется список опор, которые должны быть соединены между собой с некоторыми ограничениями. Туннельное оборудование может перемещаться только по прямой линии между точками. В любой точке города имеется место только для одного подземного кабеля, за исключением самих опор, так что никакие два кабеля не могут пересекаться.

По заданному списку точек определить наименьшее количество кабеля, необходимого для соединения каждой пары точек либо непосредственно, либо косвенно через другие пункты.

Вход. Состоит из нескольких тестов. Каждый тест начинается количеством точек n (2 ≤ n ≤ 1000) в городе. Каждая из следующих n строк содержит два целых числа x и y (-1000 ≤ x, y ≤ 1000), где (x, y) – местоположения n точек. Все точки различны. Последняя строка содержит один 0.

Выход. Для каждого теста вывести одно действительное число, равное длине кабеля, достаточного для соединения всех точек города. Вывести это число с двумя десятичными знаками. Ответ на каждый тест выводить в отдельной строке. Не выводите пустые строки между ответами на тесты.

Пример входа	Пример выхода
4 0 0 0 10 10 0 10 10 2 0 0 10 10 0	30.00 14.14

РЕШЕНИЕ

графы – алгоритм Прима

Анализ алгоритма

Для решения задачи следует найти минимальное остовное дерево. Реализуем алгоритм Прима.

Пример

Построим два графа, приведенных в примере.

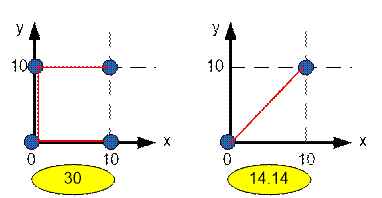
Реализация алгоритма

Объявим глобальные массивы. Координаты точек храним в (x[i], y[i]).

#define MAX 1001

#define INF 0x3F3F3F3F

int x[MAX], y[MAX];

int used[MAX], dist[MAX];

Функция dist2 вычисляет квадрат расстояния между точками i и j.

int dist2(int i, int j)

{

return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);

}

Функция Prim реализует алгоритм Прима и возвращает величину минимального остова.

double Prim(void)

{

Инициализируем массивы.

memset(dist, 0x3F, sizeof(dist));

memset(used, 0, sizeof(used));

Начинаем строить минимальный остов с вершины 0. Инициализируем dist[0] = 0, used[0] = 1. В переменной res вычисляем величину минимального остова.

double res = 0;

int i, j, cur = 0;

dist[cur] = 0;

used[cur] = 1;

Совершаем n – 1 итерацию. На каждой итерации в остов добавляем одну вершину (так что в остов еще следует добавить n – 1 вершин).

for (i = 1; i < n; i++)

{

Текущей вершиной является cur. Перебираем ребра (cur, j) и пересчитываем значение dist[j]. Таким образом dist[j] хранит текущее кратчайшее расстояние от вершины j до текущего минимального остова.

for (j = 0; j < n; j++)

if (!used[j] && (dist2(cur, j) < dist[j]))

dist[j] = dist2(cur, j);

Ищем ребро наименьшей длины, которое будет включено в остов. Для этого ищем такое наименьшее dist[j], что вершина j еще не принадлежит остову (used[j] = 0). Номер вершины с наименьшим значением dist[j] заносим в cur (она становится текущей).

int min = INF;

for (j = 0; j < n; j++)

if (!used[j] && (dist[j] < min))

{

min = dist[j];

cur = j;

}

Вершина cur включается в остов. Ребро длины sqrt(dist[cur]) добавляется к остову.

used[cur] = 1;

res += sqrt(dist[cur]);

}

return res;

}

Основная часть программы. Обрабатываем несколько тестов.

while (scanf("%d", &n), n)

{

Читаем координаты точек.

for (i = 0; i < n; i++)

scanf("%d %d", &x[i], &y[i]);

Вычисляем и выводим величину минимального остова.

res = Prim();

printf("%.2lf\n", res);

}

Реализация алгоритма – min_e / end_e

Объявим глобальные массивы. Координаты точек храним в (x[i], y[i]).

#define MAX 1010

int x[MAX], y[MAX];

int used[MAX], min_e[MAX], end_e[MAX];

Функция dist2 вычисляет квадрат расстояния между точками i и j.

int dist2(int i, int j)

{

return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);

}

Основная часть программы. Обрабатываем несколько тестов.

while (scanf("%d", &n), n)

{

Читаем координаты точек.

for (i = 0; i < n; i++)

scanf("%d %d", &x[i], &y[i]);

Инициализируем массивы.

memset(min_e, 0x3F, sizeof(min_e));

memset(end_e, -1, sizeof(end_e));

memset(used, 0, sizeof(used));

Величина минимального остова будет подсчитываться в переменной dist.

dist = min_e[1] = 0;

for (i = 0; i < n; i++)

{

Ищем вершину v с минимальным значением min_e[v] среди еще не включенных в минимальный остов вершин (для которых used[v] = 0).

v = -1;

for (j = 0; j < n; j++)

if (!used[j] && (v == -1 || min_e[j] < min_e[v])) v = j;

Включаем вершину v в остов. Добавляем в остов ребро (v, end_e[v]).

used[v] = 1;

if (end_e[v] != -1) dist += sqrt((double)dist2(v, end_e[v]));

Пересчитываем метки для ребер (v, to), исходящих из v. Перебор совершаем только по таким вершинам to, которые еще не включенны в минимальный остов (used[to] = 0).

for (to = 0; to < n; to++)

{

int dV_TO = dist2(v, to);

if (!used[to] && (dV_TO < min_e[to]))

{

min_e[to] = dV_TO;

end_e[to] = v;

}

}

}

Выводим величину минимального остова.

printf("%.2lf\n", dist);

}